Проверка распределения напряжений в бесконечном невесомом упругом полупространстве
Выполняется проверка распределения напряжений в полуплоскости от действия бесконечно протяжённой полосовой нагрузки конечной ширины. Подобное напряжённое состояние возникает в поперечных сечениях основания протяжённого ленточного фундамента.
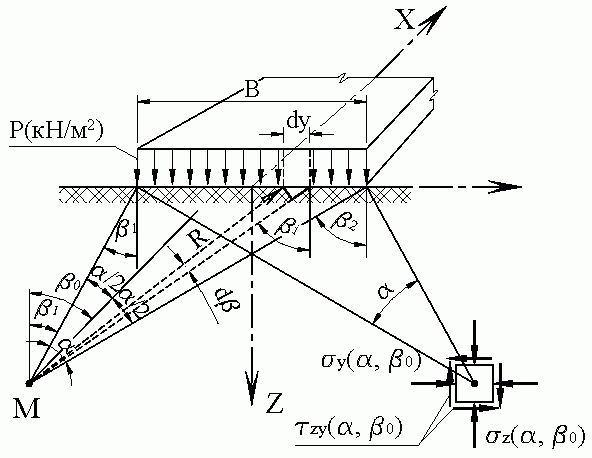
| Геометрия | ||
| h = 25 м | высота модели | |
| a = 25 м | ширина модели | |
| В = 1 м | ширина полосовой нагрузки | |
| Свойства материалов | ||
| γ = 0 кН/м³ | удельный вес | |
| E = 20000 кН/м² | модуль деформации | |
| ν = 0,45 | коэффициент Пуассона | |
| Нагрузка | ||
| P = −1 кН/м² | интенсивность нагрузки |
Результаты в SiO 2D
Ниже приводятся результаты, полученные в SiO 2D
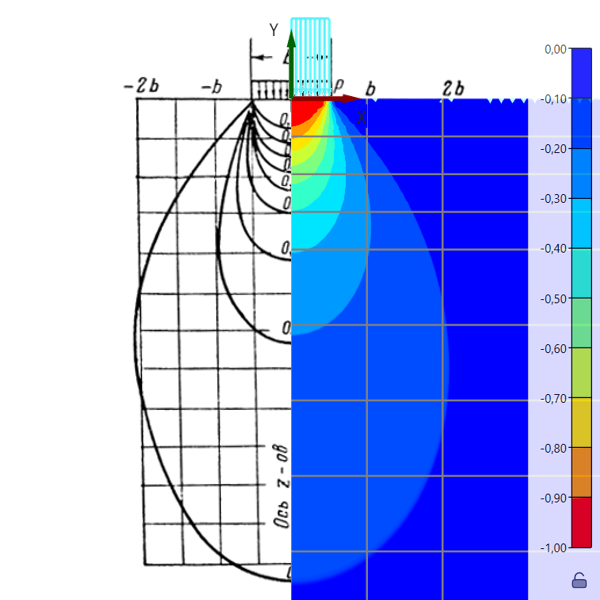
Рис. 1.3.4.
Изополя вертикальных напряжений
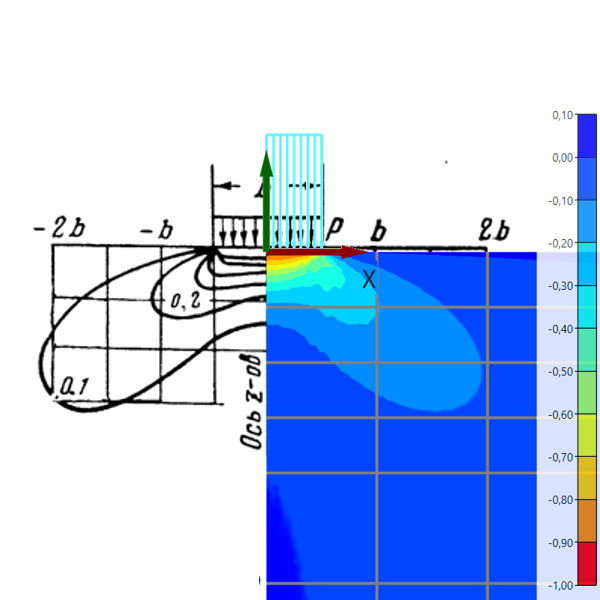
Рис. 1.3.5.
Изополя горизонтальных напряжений
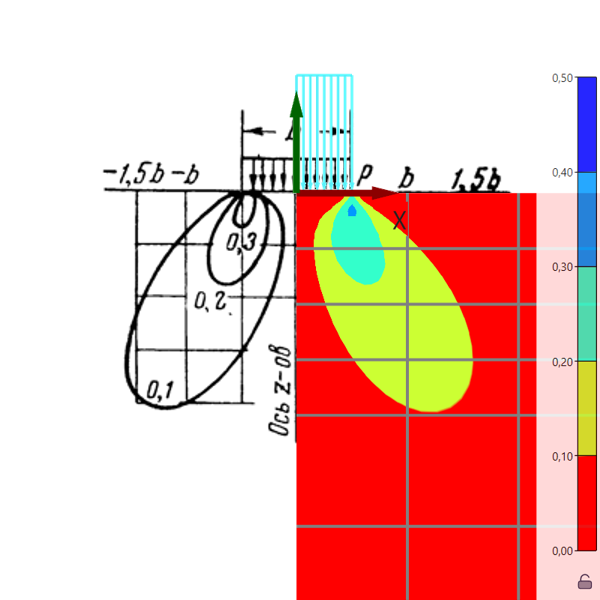
Рис. 1.3.6.
Изополя касательных напряжений
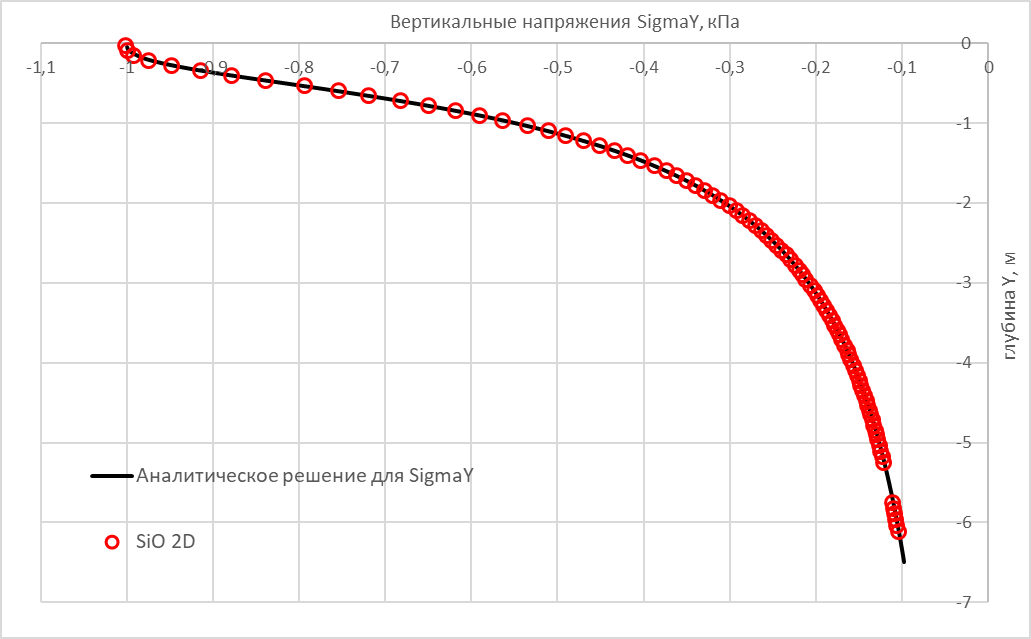
Рис. 1.3.7.
Сравнение результатов c аналитическим решением для вертикальных напряжений
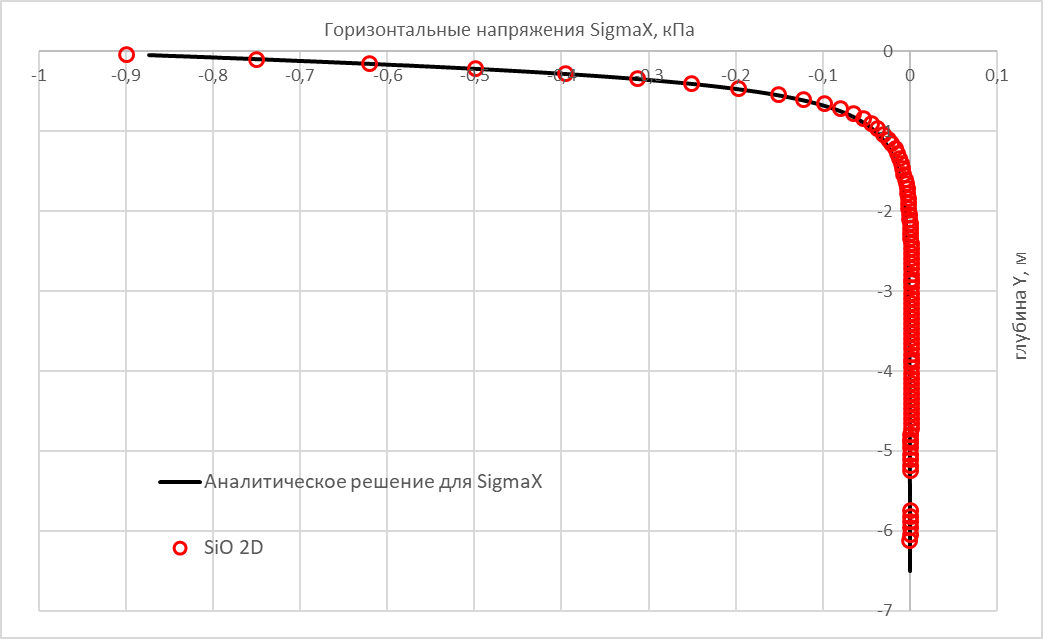
Рис. 1.3.8.
Сравнение результатов с аналитическим решением для горизонтальных напряжений
Выводы
Теоретические результаты и результаты, полученные в SiO 2D, имеют хорошую сходимость. Максимальная относительная погрешность для сравниваемых на различных глубинах величин вертикальных напряжений составляет 0,23 %.
Горизонтальные напряжения для упругой модели с постоянным значением коэффициента Пуассона в целом показывают удовлетворительную сходимость, но прямое сравнение и вычисление погрешности не выполнялось, поскольку аналитическое решение предполагает переменное значение коэффициента поперечного расширения.
| Параметр для сравнения | Эталонное решение | SiO 2D | Относительная погрешность | |
| Вертикальные напряжения σy на глубине, м: | кПа | кПа | % | |
| 0,5 | −0,81831 | −0,81641 | 0,23 | |
| 1,0 | −0,54982 | −0,54906 | 0,14 | |
| 1,5 | −0,39582 | −0,39558 | 0,06 | |
| 2,0 | −0,30575 | −0,30574 | 0,00 | |
| 3,0 | −0,20837 | −0,20867 | 0,14 |
Примечание
Результаты, представленные в отчёте, могут незначительно отличаться от результатов, полученных в других версиях программы.
