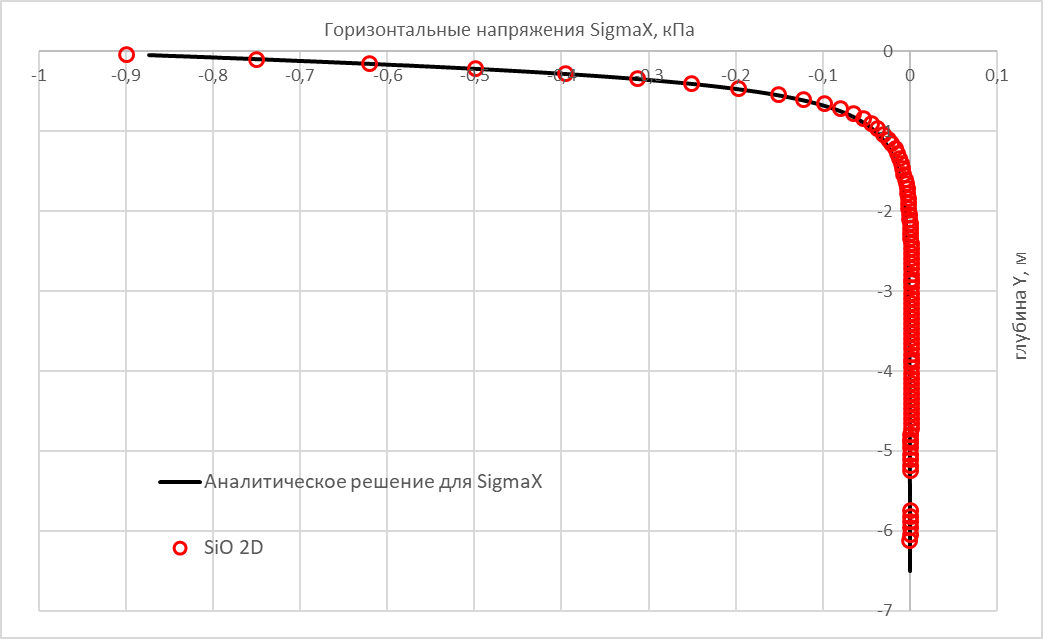
Стационарная фильтрация в однородном массиве грунта

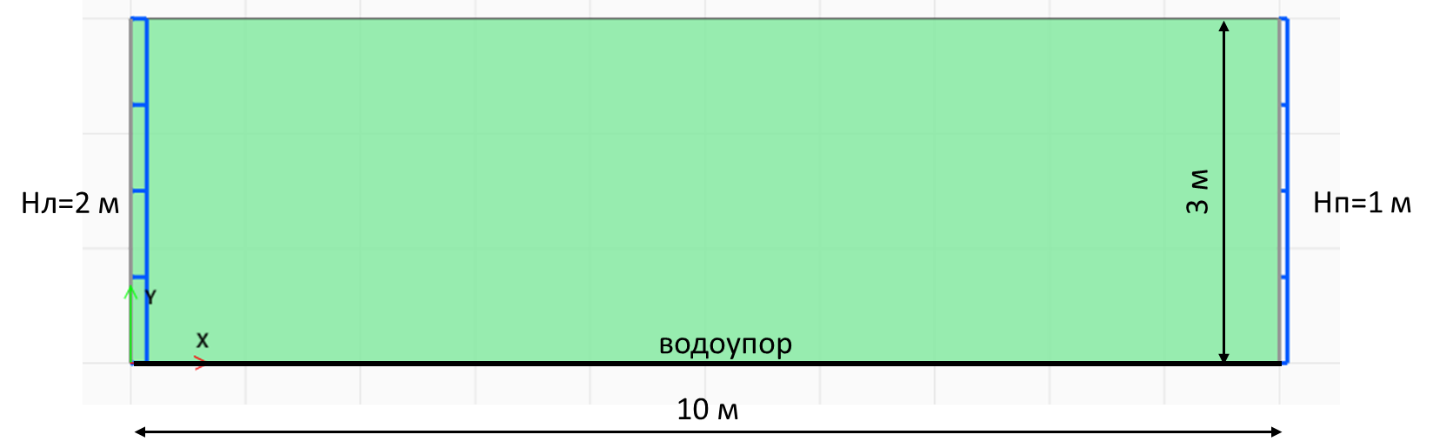
Исследуется правильность реализации расчёта стационарной фильтрации в SiO 2D. В примере верифицируется результирующий уровень воды и величина общего расхода.


	Геометрия
	L = 10 м	путь фильтрации
	Hл = 2 м	отметка УГВ слева
	Hп = 2 м	отметка УГВ справа
	Свойства материалов
	γ = 0 кН/м³	удельный вес
	E = 1 кН/м²	модуль деформации
	ν = 0	коэффициент Пуассона
	kx = ky = 1 м/сут	коэффициенты фильтрации

Эталонное решение

В предположении гидростатического распределения порового давления для каждого вертикального сечения общий расход через слой q можно приближенно определить по формуле Дюпюи для безнапорной фильтрации (Dupuit, 1863) (рис. 5.1.2):

q = k * (h1^2 - h2^2) / 2L

где k – коэффициент фильтрации, L – длина слоя, h1 и h2 – напор грунтовых вод на левой и правой границах, соответственно.

Для данной ситуации, согласно приведённой формуле, расход равен 0,150 м³/сут/м.

По уравнению Дюпюи можно построить кривую свободной поверхности грунтового потока. Для этого необходимо иметь данные о превышении свободной поверхности h1 и h2 над водоупором в скважинах 1 и 2, расположенных в начале и в конце рассматриваемого участка (рис. 5.1.3).

Таким образом, величина h может быть определена по формуле:

h = (h2^2 + 2x * q / k)^0.5

Вычислим высоту h для рассматриваемого примера в трёх различных сечениях:


	x, м	h, м
	8	1,84
	5	1,58
	2	1,26

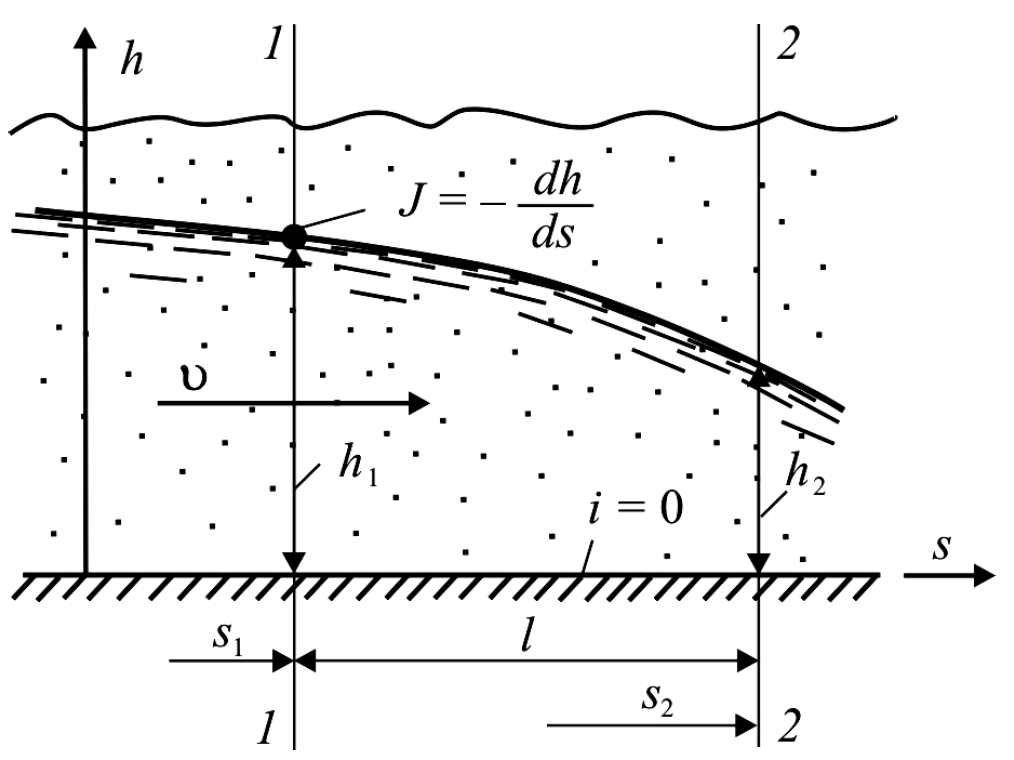
Рис. 5.1.2

К интегрированию дифференциального уравнения плавноизменяющегося безнапорного движения грунтовых вод (для плоской задачи) при горизонтальном водоупоре

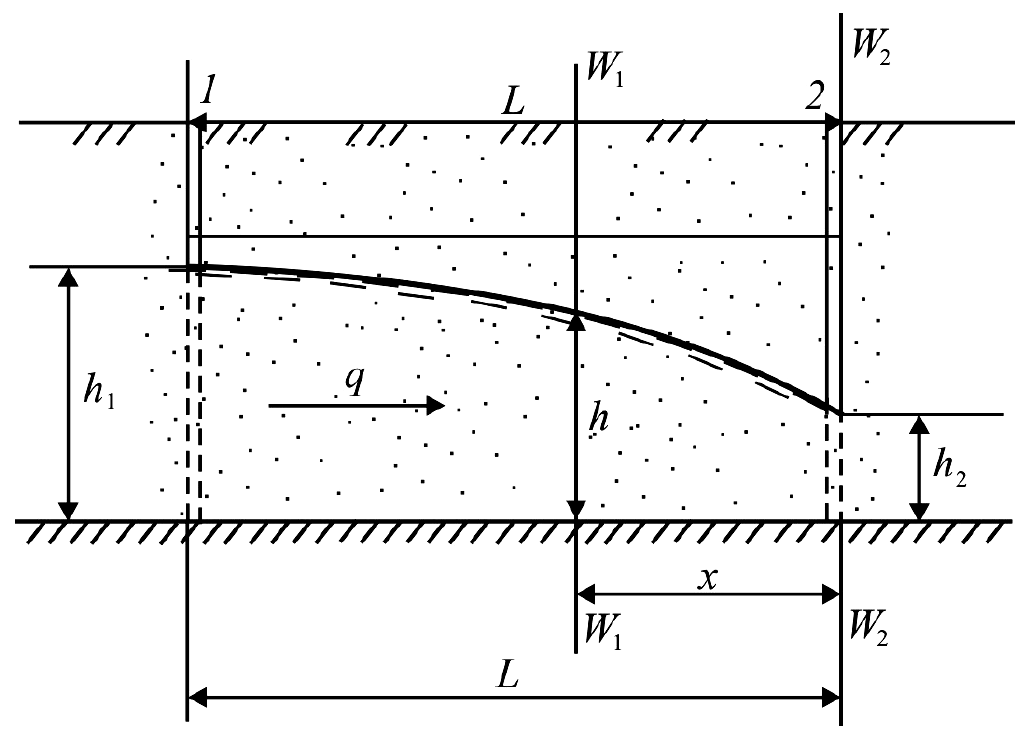
Рис. 5.1.3

К построению кривой свободной поверхности грунтового потока (кривой депрессии)

Результаты в SiO 2D

Ниже приводятся результаты, полученные в SiO 2D

Рис. 5.1.4. Изополя поровых давлений

Рис. 5.1.5. Изополя напоров

Рис. 5.1.6. Изополя скоростей фильтрации

Рис. 5.1.7. Суммарный расход в различных сечениях

Рис. 5.1.8. Поровые давления в различных сечениях

Выводы

Теоретические результаты и результаты, полученные в SiO 2D, близки. Относительная погрешность для общего расхода составляет 3,3 %, максимальная относительная погрешность для высоты кривой депрессии — 0,8%.


Параметр для сравнения	SiO 2D	Эталонное решение	Относительная погрешность, %
Общий расход q, м³/сут/м	0,155	0,150	3,3
Отметка кривой депрессии
в координате X = 8 м	1,85	1,84	0,5
в координате X = 5 м	1,58	1,58	0,0
в координате X = 2 м	1,25	1,26	0,8

Примечание

Результаты, представленные в отчёте, могут незначительно отличаться от результатов, полученных в других версиях программы.

Остались вопросы?

Заполните форму и получите полный верификационный отчёт. Технические специалисты готовы ответить на ваши вопросы о программе

Запросить отчёт Запросить демо

Стационарная фильтрация в однородном массиве грунта

Эталонное решение

Рис. 5.1.2

Рис. 5.1.3

Результаты в SiO 2D

Выводы

Примечание

Остались вопросы?

Контакты

О программе

Помощь

Компания