Одномерная консолидация

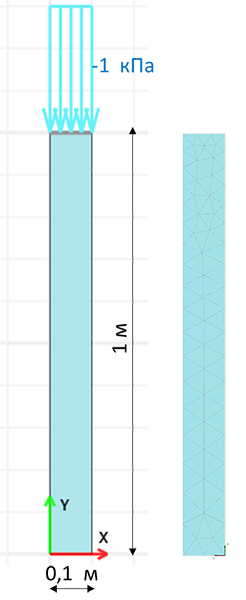
Проверяется реализация расчёта консолидации в SiO 2D: исследуется изменение избыточного порового давления при нагружении в грунтовой колонке высотой 1,0 м и шириной 0,1 м, наверху которой приложена вертикальная нагрузка. В примере верифицируется распределение относительного избыточного порового давления во времени и в зависимости от глубины.

Рис. 9.1.1

Расчётная схема


	Геометрия
	h = 1,0 м	высота модели
	b = 0,1 м	ширина модели

Свойства материалов


№	Параметр	Значение	Наименование
1	γ	0 кН/м³	удельный вес
2	E	1000 кН/м²	модуль деформации
3	ν	0	коэффициент Пуассона
4	kx	0,001 м/сут	коэффициент фильтрации в горизонтальном направлении
5	ky	0,001 м/сут	коэффициент фильтрации в вертикальном направлении
6	B	0,9933	параметр Скемптона

Граничные условия

Деформационные граничные условия


	Граница	Тип
	Верхняя	Свободная
	Правая	Закреплённая по горизонтали
	Нижняя	Закреплённая по горизонтали и вертикали
	Левая	Закрепленная по горизонтали

Фильтрационные граничные условия


	Граница	Тип
	Верхняя	Открытая
	Правая	Закрытая (непроницаемая)
	Нижняя	Закрытая (непроницаемая)
	Левая	Закрытая (непроницаемая)

Эталонное решение

Искомое значение: распределение относительного избыточного порового давления по глубине и во времени:

p / p0 (z, t)

Одномерная консолидация грунта может быть описана с помощью следующего дифференциального уравнения для избыточного порового давления p:

∂p/∂t = c_v (∂^2 p) / (∂z^2 )

где z – глубина над нижней границей грунта:

z = H − y

Степень консолидации c_v определяется как:

c_v = (k ⋅ E_oed) / γ_w

E_oed = (1−ν') ⋅ E' / ( (1+ν') ⋅ (1−2ν') )

Аналитическое решение этого уравнения в виде относительного избыточного порового давления p⁄p_0 как функции времени t и глубины z дано в работе Verruijt (2001):

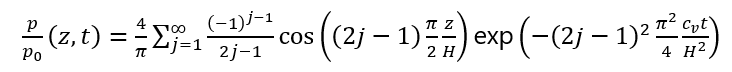
Это решение, а также результаты, полученные в SiO 2D, представлены на рисунках 9.1.2–9.1.4. Каждый из рассмотренных периодов консолидации представляет собой участок в виде безразмерного фактора времени Тv, определенного как Tv = (c_v⋅t)/(H2). Напор Н равен высоте грунтовой колонки. Глубина z нормализуется по H.

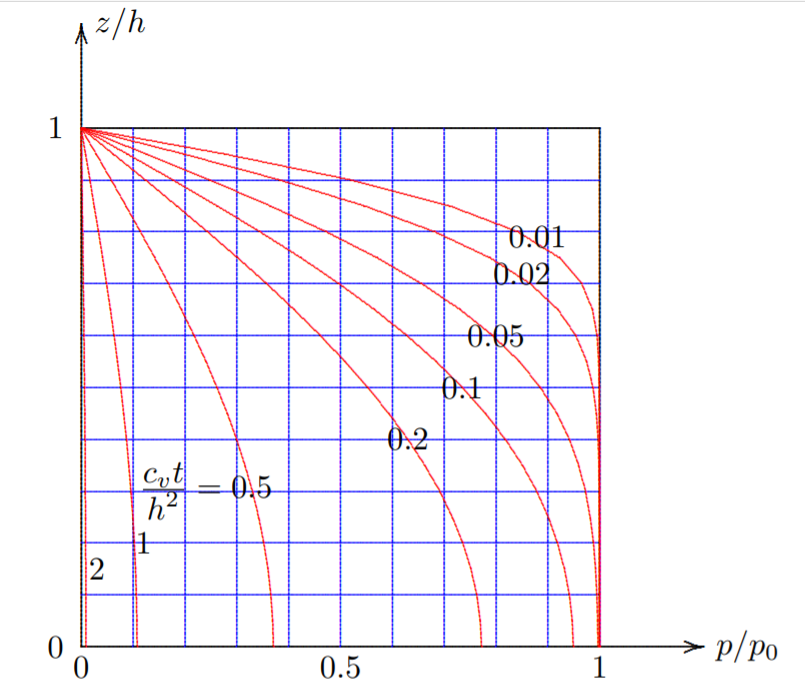
Рис. 9.1.2

Аналитическое решение (Verruijt, 2001)

Результаты в SiO 2D

Ниже приводятся результаты, полученные в SiO 2D.

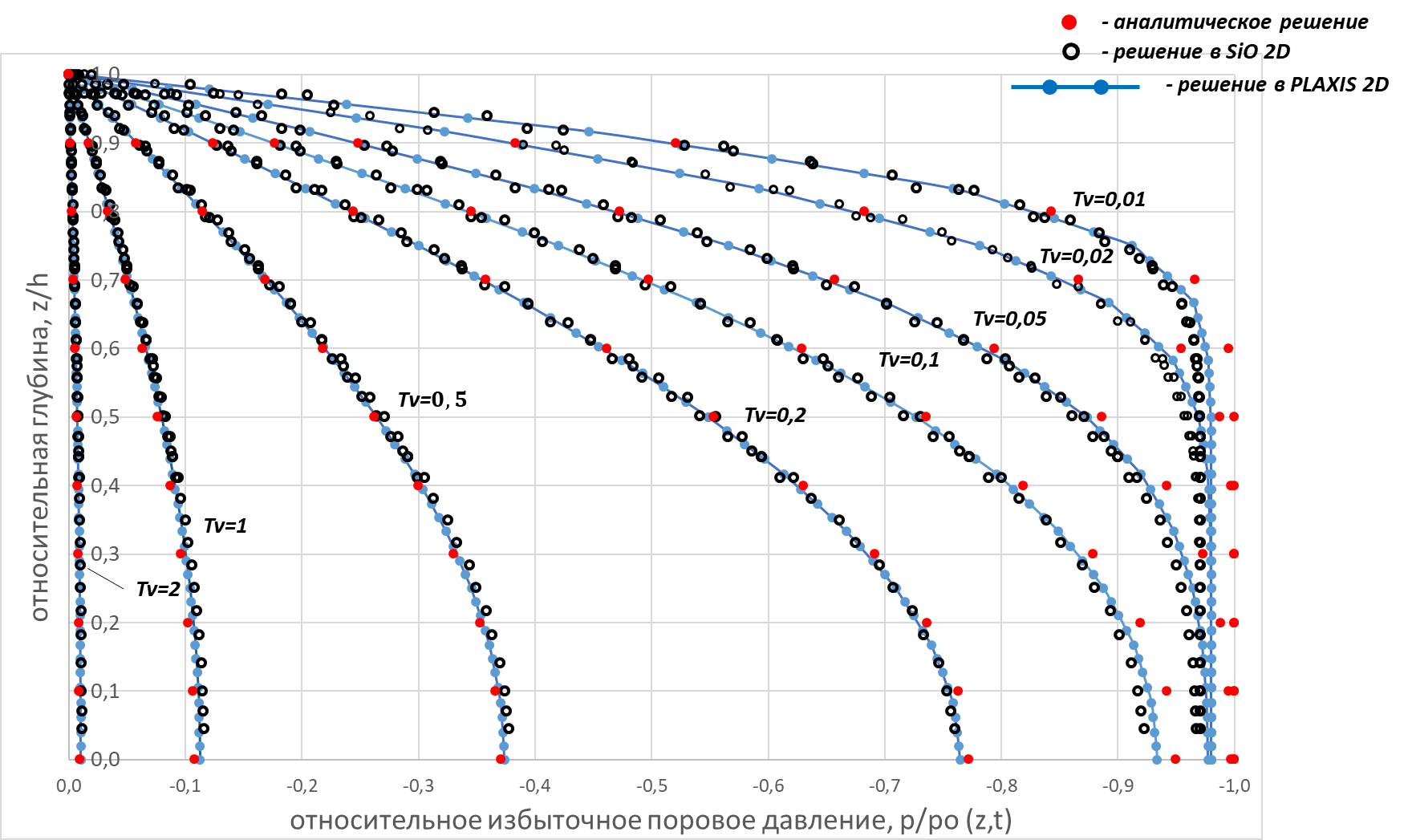
Рис. 9.1.3

Развитие относительного избыточного порового давления p/p0 во времени (Тv) и в зависимости от глубины (z/H), полученное в SiO 2D и аналитически

Рис. 9.1.4

Эпюры избыточного порового давления
по вертикальному сечению грунтовой колонки в SiO 2D

Выводы

Рассчитанные максимальные погрешности для каждой кривой на рис. 9.1.3 представле-ны в таблице ниже.


Tv	Эталонное решение	SiO 2D	∆(%)
0,01	−0,9953	−0,9649	3,06
0,02	−0,8664	−0,9392	8,40
0,05	−0,7941	−0,7674	3,37
0,10	−0,6286	−0,6076	3,34
0,20	−0,4616	−0,4474	3,09
0,50	−0,0580	−0,0608	4,78
1,00	−0,0169	−0,0186	10,35

Теоретическое решение и результаты, полученные в SiO 2D, хорошо согласуются. Максимальные относительные погрешности для рассмотренного консолидационного расчёта варьируются от 3,06 до 10,35 %. Важно отметить, что расхождения вызваны тем, что изначально рассчитанное избыточное поровое давление в SiO 2D зависит от параметра Скемптона и составляет 0,993 × p_внеш, вместо 1.0 × p_внеш (как в строгом аналитическом решении). Это связано с тем, что поровая вода в SiO 2D не является полностью несжимаемой. По этой же причине результаты в программе PLAXIS 2D также имеют небольшие расхождения с аналитическим решением и более близки к результатам в SiO 2D.

Примечание

Результаты, представленные в отчёте, могут незначительно отличаться от результатов, полученных в других версиях программы.

Остались вопросы?

Заполните форму и получите полный верификационный отчёт. Технические специалисты готовы ответить на ваши вопросы о программе

Запросить отчёт Запросить демо